«Uma pergunta curiosa» - Resposta
SOLUÇÃO do problema colocado em: http://sorumbatico.blogspot.com/2005/12/uma-pergunta-curiosa.html
A ciclóide:
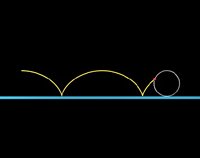Um ponto de uma circunferência rodando (sem escorregamento) sobre uma linha gera uma curva chamada ciclóideNOTA: Atenção aos preciosos Comentários-2 e 3 feitos sobre este assunto.
Afixado por: Carlos Medina Ribeiro às 22:23
3 Comments:
NOTA: No texto que acompanha o desenho diz-se "meio-ciclo", mas não sei se essa condição será necessária.
É possível que um arco menor já satisfaça as condições exigidas.
Não sei...
Também é chamada de Curva Braquistócrona (não tenho a certeza se é assim que se escreve em Português) ou curva da mais rápida descida.
Na Wikipedia há uma artigo sobre esta:
http://en.wikipedia.org/wiki/Brachistochrone
E aqui: http://home.ural.ru/~iagsoft/BrachJ2.html
está uma aplicação de demonstração em Java.
O arco de curva não tem de ser obrigatoriamente uma meia ciclóide.
Vejamos : numa qualquer ciclóide, a altura do vão é 2.R, diâmetro da circunferência que lhe serve de geratriz e a abertura é 2.Pi.R, exactamente o perímetro da mesma circunferência. (Pi é o nosso "velho" 3,141592654...).
O segmento de recta que une o ponto de "partida" da ciclóide com o ponto que marca a meia ciclóide (neste caso, o ponto mais baixo) faz com a vertical um ângulo cuja tangente trigonométrica será de Pi.R a dividir por 2.R, ou seja, Pi/2.
Logo, será um ângulo de aprox. 57,518 graus.
Apenas neste caso se terá uma meia ciclóide como solução para o Problema da Braquistócrona, proposto à comunidade matemática, em 1696, pelo Sr. Jean Bernoulli (1667-1748).
Como se depreende, aqueles que resolveram o problema encontraram uma curva, a ciclóide, que já era conhecida desde há muito.
Curiosamente, é também a ciclóide que satisfaz o problema da tautócrona, a curva ao longo da qual uma esfera demora o mesmo tempo a chegar ao ponto mais baixo qualquer que seja o ponto da curva de onde seja largada. Isto foi descoberto pelo velho Huygens e, como não podia deixar de ser, foi logo aproveitado na regulação dos relógios de pêndulo. Bons tempos ...
Mas o mais relevante disto tudo é que o problema da braquistócrona, bem como o problema da tautócrona, são satisfeitos pela ciclóide porque o movimento de queda de um corpo no campo gravitacional da Terra, desprezando os atritos, segue uma lei simples, descoberta por Galileu, em que a velocidade adquirida é proporcional à raiz quadrada do espaço percorrido. Se não fosse assim, outras curvas cantariam ...
Jorge Oliveira
Enviar um comentário
<< Home