Pergunta de algibeira

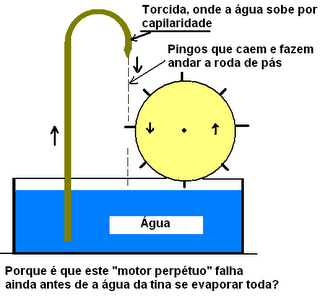
A comparação não é muito exacta, mas dá para ter uma ideia do vício-de-raciocínio que leva algumas pessoas a pensar que a água pode pingar indefinidamente do lado direito da torcida (desenho de cima) - fazendo andar a roda com a energia obtida a partir da força da capilaridade.
Há inúmeros exemplos de problemas semelhantes, relativos a motores perpétuos - funcionando, supostamente, com a força da gravidade, de ímanes, etc.
NOTA: o conceito de motor perpétuo não deve ser confundido com o de movimento perpétuo - no primeiro caso, trata-se de algo de onde se pretende retirar energia indefinidamente sem lhe fornecer nenhuma do exterior - o que, infelizmente, não é possível. Inversamente, o movimento dos planetas em torno do Sol (ou dos electrões em torno dos núcleos atómicos) pode ser considerado, pelo menos à escala humana, como sendo um movimento perpétuo - e esse, sim, existe.

9 Comments:
Porque a partir de um determinado momento, a posição das pás é tal, que nenhuma é mais " apanhada " pelas gotas que caem.
A explicação é AINDA mais fácil, pois as pás nem sequer chegam a mexer-se.
Porquê?
Insuficiente energia das gotículas para vencer a inércia das pás?
Só pode ser...
A partir do momento em que toda a torcida fique húmida, "a capilaridade pára" e não existirá acumulação de água para formar pingos de água e pingar. Mas se funcionasse dava jeito, mesmo muito jeito!!
De facto, o que sucede é que a água, simplesmente, NÃO PINGA!
Basta pensar assim (em linguagem simples):
Se a capilaridade "tem força" para elevar a água do lado esquerdo, então ainda "tem mais força" para a não deixar cair.
Neste momento lúdico e de pura diversão, permita-me que discorde.
A torcida vai ficando saturada de água, completamente encharcada, e a força gravítica no troço descendente acabará por fazer desprender as gotas. E pinga!
Um abraço cibernáutico.
Sim, é verdade o que diz André Felício e não é verdade o que diz o Anónimo das 11h17m.
A água sobe até ao ponto mais alto e, possivelmente, nem vai para a parte do lado direito do "arco".
O motivo é que a capilaridade é uma força que se exerce CONTRA a da gravidade.
Quem tiver dúvidas, pode experimentar com uma toalha ou com um guardanapo de papel totcidos:
Faz um "U", mete uma ponta dentro de um recipiente com água, e a outra ponta deixa-a MAIS ALTA do que o nível da água.
Verá que não cai uma gota.
-
Este exemplo é um dos mais conhecidos como demostração de que não existem motores perpétuos.
Incluí um desenho novo (parágrafo 2), com a analogia de um sifão.
Pode não ser grande coisa como comparação, mas quem achar que, embora a coisa não funcione com um sifão, funciona com uma torcida (e devido à capilaridade associada) pode, como atrás se diz, fazer a experiência com um lavatório cheio de água e uma toalha bem torcida:
Mergulhará, na água, uma ponta da toalha e manterá a outra ponta mais acima.
A água, de facto, subirá nela até a encharcar totalmente.
A decepção vem depois:
Virar para baixo a ponta que está de fora (mantendo-a ACIMA do nível da água) e sentar-se confortavelmente à espera que a água pingue...
Num post mais recente, mostra-se o famoso "motor" com íman, que também aparece sempre que se fala de "motores" que usam campos-de-forças sem fornecimento de energia exterior.
Enviar um comentário
<< Home