Um problema de Geometria
Afixado por: Carlos Medina Ribeiro às 17:11
16.11.06
Contribuidores
- A. M. Galopim de Carvalho
- António Barreto
- Antunes Ferreira
- Nuno Crato
- Guilherme Valente
- Alice Vieira
- J. L. Saldanha Sanches
- Carlos Medina Ribeiro
- Joaquim Letria
- Carlos Barroco Esperança
- Helena Roseta
- Pedro Barroso
- João Duque
- Nuno Brederode Santos
- Alfredo Barroso
- Maria Filomena Mónica
- Manuel João Ramos
- Carlos Pinto Coelho
Artigos anteriores mais recentes
- O «Bando do faz-de-conta» voltou a atacar?!
- TUDO PREJUÍZO
- «Almanach Bertrand» - O humor em 1930
- Há cada maduro!...
- «Almanach Bertrand» de 1930
- E já que falámos de estradas...
- HCESAR
- Já está nos "Favoritos"!
- A malta come-tudo...
- Ainda a sinistra...
7 Comments:
25
He; He, He...
O raio da coisa noutra posição fica diferente não é?
Até parece mais pequenino...
Certo.
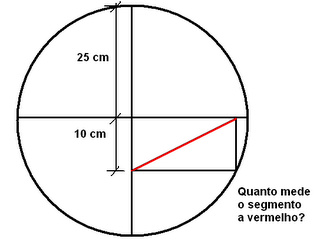
O que torna este problema curioso é o facto de as pessoas, muitas vezes, começarem a fazer contas, quando a resposta está no facto de a outra diagonal do rectângulo ser também um raio da circunferência.
E ainda:
Quando nos dão problemas para resolver, estamos habituados a que os "dados" sejam os necessários e suficientes.
Neste caso, os 10cm não interessam para nada, pois qualquer valor entre 0 e 25 serviria.
Eu fiz contas, claro que indo buscar a outra diagonal do rectângulo. Eh Eh Eh!
O problema podia também ser posto de outra forma:
«Qual o comprimento dos 2 segmentos em que segmento a vermelho divide o raio "horizontal"?»
Aqui, sim, já entra o Pitágoras, e a resposta é:
22,9cm e 2,1cm (aprox.)
Não querendo ser picuinhas, mas ainda assim sendo-o, o segmento na figura que pretende indicar o comprimento do raio da circunferência como 25 cm devia estar sobre o diâmetro vertical da circunferência, caso contrário mede menos de 25 cm...
Enviar um comentário
<< Home