Puxando pela cabecinha...
COMO é que é possível alguém partir de um ponto, andar 1000 quilómetros para Sul, depois 1000 para Oeste e finalmente 1000 para Norte, acabando por se encontrar novamente no ponto de partida?
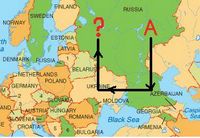
(Neste mapa está representado um exemplo de um ponto, A, que NÃO satisfaz as condições exigidas)
As pessoas normais dizem que é impossível, enquanto as mais inteligentes respondem que é possível, desde que o ponto de partida seja o Pólo Norte - o que é verdade.
Ora o problema é que, além do Pólo Norte, há (pelo menos) mais um ponto no Globo que satisfaz essa condição.
QUAL É ELE?
--
(As respostas foram dadas aqui em "Comentários", e um desenho explicativo foi metido em post no dia 12 Maio, às 22 h 05m).

9 Comments:
Na realidade, não há só mais «UM» ponto que satisfaz...
Por incrível que pareça, até há mais do que um.
Quando se diz «1000 km», trata-se apenas de um exemplo.
A questão é válida para qualquer outro valor:
«Andar n km para Sul, n para Oeste e n para Norte - e encontrar-se novamente no ponto de partida».
Caro Pólux:
No seu raciocínio, encontra, é claro, infinitas soluções, mas todas elas a partir do Pólo Norte.
Eu talvez não tenha explicado bem:
O que pergunto é quais são os outros pontos "A", DE PARTIDA SEM SER O PÓLO NORTE.
(Veja a resposta a seguir á sua - quente... quente...)
Caro Pólux,
Desculpe, mas eu ainda estava a dormir quando li a sua resposta!
É que a segunda parte está certa!!
O paralelo que está 1000 km a norte de um outro com 1000 km de perímetro é o lugar-geométrico de pontos "A" que satisfazem a condição.
O PROBLEMA É QUE HÁ AINDA MAIS CASOS!!!
E esta?!
Caro amigo "zxcv":
Certíssimo, mas há AINDA MAIS FAMÍLIAS DE SOLUÇÕES...
Estou bem arranjado! Não encontro mais nenhuma solução!
Exceptuando o pólo Norte e os pontos dos meridianos antes referidos como pontos de partida, parece que a única maneira de realizar o percurso pedido é descrever um triângulo esférico equilátero ABC, o que poderia fazer de 'infinitas maneiras', não fora haver as restrições de orientação impostas: o lado AB tem que se conter num meridiano que passe pelos pólos e o mesmo sucede com o lado CA. Assim, só existe um tal triângulo bom: o que tem o vértice A coincidente com o pólo Norte, ponto esse já fora de questão.
Que charada!
Será que o movimento de rotação da Terra é para aqui chamado e possamos 'andar parados'?
A ser assim, o problema pode solucionar-se de outro modo e terá muitas, mesmo muitas, soluções, a saber: todos os pontos que distam pelo menos 1000 Km do pólo Sul. Como? Basta que partamos de um tal ponto, A, caminhemos 1000 Km para Sul, 'estacionemos' num ponto B, aguardemos aí o tempo necessário para que a Terra nos arraste 1000 Km no seu movimento de rotação (tal tempo de espera varia com o ponto B, naturalmente) e depois façamos o inverso do trajecto inicial, para regressar a A.
Esta resposta é pouco ortodoxa, mas em charadas tudo é possível!
Quando quiserem, indico a resposta que falta (pois já aqui foram dadas várias certas).
A mais próxima é esta:
«O paralelo que está 1000 km a Norte de um outro com 1000 km de perímetro é o lugar-geométrico de pontos "A" que satisfazem a condição».
Mas, como digo, há uma outra, muito parecida - É essa que falta.
Penso que acabei de encontrar mais uma 'grande infinidade' de pontos que satisfazem a questão, a acrescentar aos dos dois pararelos do comentário das 4:38 AM:
.todos os pontos do paralelo 1000 Km a Norte do paralelo de perímetro 500 Km (a justificação é similar à feita para o paralelo de perímetro 1000 Km, só que em vez de 1 se devem dar 2 voltas para regressar ao ponto B);
.todos os pontos do paralelo 1000 Km a Norte do paralelo de perímetro 250 Km (a justificação é similar à do paralelo de perímetro 1000 Km, só que em vez de 1 se devem dar 4 voltas para regressar ao ponto B);
.todos os pontos do paralelo 1000 Km a Norte do paralelo de perímetro (1000:(2^n)) Km (a justificação é similar à do paralelo de perímetro 1000 Km, só que em vez de 1 se devem dar 2^n voltas para regressar ao ponto B -- n designa um número inteiro positivo qualquer);
...
Nota: Estes paralelos, lugares geométricos de pontos solução, são do hemisfério Sul.
Caro "zxcv":
BINGO!!!
CMR
Enviar um comentário
<< Home