Um problema «musical»
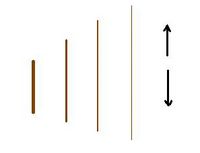
IMAGINE-SE um elástico que se mantém esticado pelas suas extremidades e se faz vibrar como uma corda de viola, forçando-o a emitir um som.
Pergunta-se: se ele for esticado ainda mais, o novo som é mais agudo ou mais grave do que o anterior?
E porquê?
--
NOTA: Pronto! A resposta está dada no "Comentário-19", das 8h46m PM.

23 Comments:
Eu penso que será mais agudo.
O som será uma progação de ondas circulares crescentes (tipo pedra no charco), partindo do princípio que os sons agudos apresentam menor espaçamento entre ondas (frequência mais elevada) e que ao esticarmos o fio a frequência do do som sobe, o som será mais agudo.
Além disso possuo um baixo e à medida que estico a corda o som fica mais agudo.
Obrigado, amigo.
Mas, quer no seu baixo, quer na generalidade dos instrumentos de cordas, o comprimento (da parte das cordas que vibra) é constante.
O que varia é a tensão.
Não é esse o caso neste exemplo.
--
Amanhã darei aqui a resposta e a explicação.
Engraçado, parece que o som se mantém. Mas como acabei de rebentar um elástico nos dedos, não me apetece experimentar mais. :-)
De facto, embora possa haver algumas pequenas diferenças (pelo facto de o elástico não ser homogéneo), o som mantém-se.
O "porquê" será dado amanhã aqui.
Concordo que deve ser mais agudo. Isto deve-se a uma maior tensao a que a corda fica submetida, o que resulta numa frequencia, ou vibraçoes por segundo, mais alta.
Por sua vez, o elastico esticado tem uma menor superficie, por isso creio que a vibraçao transmitida para o ar, e por consequência ao timpano, vai ter propriedades um pouco diferentes.
Certo Carlos...mas eu também não disse que o comprimento da parte da corda que vibra é diferente, eu estaria a referir ao espaçamento entre as sucessivas ondas circulares que se propagam.
http://www.feiradeciencias.com.br/sala10/10_T01.asp
Caro João Dias,
As ondas que se propagam não são circulares porque o elástico não é um ponto vibratório.
Caro Medina Ribeiro,
A frequência mantém-se porque num material perfeitamente elástico a taxa a que ele devolve a energia para o meio é inversamente proporcional à energia acumulada. Se o elástico estiver um pouco esticado tem uma bocado mais de energia acumulada e por isso devolve-o a uma taxa maior, mas como é mais comprido a frequência mantém-se.
acima é óbviamente 'directamente proporcional'
Amigos,
Já que isto está tão animado, vamos esperar até amanhã para dar a resposta e respectiva justificação.
Mas a explicação está simplesmente relacionada com o seguinte:
1 - O elástico, nas condições indicadas no problema, funciona como uma "corda vibrante".
2 - O valor da frequência do som emitido (à parte harmónicas, é claro) é dada pela chamada "equação da corda vibrante", que tem em conta:
A)A massa por unidade de comprimento
B) A tensão
C) O comprimento
As ondas sonoras não são circulares?
De certeza?
Na teoria de Doppler os esquemas que aparecem das ondas sonoras é a de círculos sucessivos cada vez maiores...agradecia esclarecimentos porque, sinceramente, estou a ficar algo confuso.
Amigo João Dias,
O melhor será fazer uma pesquisa na Internet em "ondas", "cordas vibrantes", etc., porque aqui o espaço não dá para muito.
No entanto, as ondas são fenómenos oscilatórios que se propagam.
1 - Uma pedra atirada para a água é o exemplo clássico: gera ondas circulares.
2 - Uma onda sonora ou luminosa, emitida num ponto do espaço, gera ondas esféricas.
3 - Uma mola que se comprime axialmente e depois se larga gera ondas ao longo do seu comprimento.
4 - Uma corda que se abana, é percorrida por ondas que podem ir de uma ponta à outra, embater no extremo e voltar para trás.
5 - No caso em apreço, trata-se de uma "corda vibrante":
Um corpo elástico, longo e fino, que está fixado nos seus extremos e se faz oscilar LATERALMENTE, por acção de uma força perpendicular ao seu eixo.
João,
As ondas não são perfeitamente circulares porque um elástico não é uma esfera. É certo que numa zona mais afastada da vibração a viscosidade do ar as tende a 'arredondar' e uma boa aproximação é um circulo/esfera, mas isso é numa zona mais afastada. Próximo elas têm uma forma bastante complexa.
Certo António, mas o efeito de doppler explica o fenómeno do mesmo som nos parecer mais grave à medida que se afasta o emissor e mais agudo à medida que se aproxima, logo, visto estar afastado do emissor, a propagação do som é representado por sucessivos círculos crescentes (2D). É utilizado um esquema 2D para visualizar o fenómeno, e as esferas vistas a 2D apresentam-se como círculos (naturalmente) daí eu ter falado em círculos e não em esferas.
Mas como na explicação do efeito de Doppler aparece a explicação de que as ondas sonoras se comprimem (aproximam entre si) ao aproximarem do receptor e isso confere um som mais agudo, eu tentei fazer a falhada analogia entre esta situação.
Está uma imagem elucidativa do que eu estou a tentar falar neste site:
http://www.espinoso.org/biblioteca/OrigenUniverso.htm
Não sei o que o efeito de doppler tem a haver com a forma das ondas. Não é prssuposto largar-se o elástico a vibrar.
Amigo Carlos,
parece que já vi a equação será V=raiz(T/u)?
Se for esta aqui vai uma hipotética explicação:
u- densidade linear
T- tensão
a tensão aumenta, a densidade linear diminuir visto que o comprimento aumenta e a massa mantém-se. A velocidade deverá manter-se se a subida de tensão for proporcional á descida de densidade linear, é o que parece ser o caso. Se a velocidade se mantém a tonalidade do som deverá manter-se.
O problema será que não me passou pela cabeça associar velocidade à variação da tonalidade do som e me esqueci do aumento de comprimento.
Pois, António, eu referi que a analogia não foi bem conseguida. Mas no efeito de Doppler é dito que quando o comprimento de onda é mais curto o som é mais agudo, eu usei isso para criar o raciocínio.
E o som propaga-se em ambos os casos certo? Apesar do emissor se manter imóvel.
Caros amigos,
Acho que já podemos encerrar o assunto, pois o essencial já foi dito.
Mas, antes disso, um pequeno reparo:
Vi aqui alguma confusão entre "velocidade" e "frequência". Mais ainda quando se aparece a falar do efeito Doppler.
Este "efeito" só interessa para fontes sonoras em movimento em relação a um observador.
Não tem a ver com o som emitido por uma espécie de "corda de viola" feita com um elástico - e este é que era o problema posto.
RESUMINDO:
Ao esticar o elástico, a frequência de vibração é sujeita a efeitos contraditórios:
A) Pelo facto de o elástico ficar mais fino, o som seria mais AGUDO.
B)Pelo facto de aumentar o comprimento, o som seria mais GRAVE.
C) Pelo facto de aumentar a tensão, o som seria mais AGUDO.
--
Ora, os efeitos que tornam o som mais agudo "funcionam" com a raiz quadrada, enquanto o efeito que o torna mais grave é linear.
Assim (e em termos puramente teóricos), os 3 efeitos anulam-se e a frequência mantém-se.
--
OBRIGADO A TODOS!
EM BREVE HAVERÁ MAIS!
--
(Para quem não viu na altura: em posts anteriores, há outras adivinhas curiosas)
Peço desculpa por ser tão sarna mas é dificíl admitir que não percebemos nada da questão.
Mesmo assim acho que não perceberam o meu raciocínio, eu não queria introduzir o "efeito" neste caso particular, é bastante óbvio que o emissor (elástico) não está em movimento. Sabendo que, esticado, o elástico teria uma oscilação menor eu fiz o raciocíno (incompleto) de que este ficaria mais agudo, aliás parece-me esse o raciocínio da alinea c.
Quanto maior o comprimento de onda menor será a frequência, como o espaçamento entre os círculos (2D) sucessivos representa o comprimento de onda, acho perceptível a razão de o esquema ajudar a perceber porque um som será mais grave ou agudo, sendo que obviamente este facto por si só não dava para responder a questão.
Resumindo:
Eu não queria que corroborassem o meu erro, queria que o compreendessem e que eu apenas o tinha usado para perceber a diferença entre um som grave e agudo.
Peço-vos que consultem este site e verifiquem a parte que diz: "El observador en reposo". Apenas para que possam visualizar a noção gráfica de comprimento de onda.
http://www.edu.aytolacoruna.es/aula/fisica/teoria/A_Franco/ondas/doppler/doppler.html
O endereço indicado pelo amigo João Dias no "post" anterior é muito interessante.
Vale a pena visitá-lo e fazer e experiência virtual que lá se mostra.
Obrigado e um abraço.
Mais uma achega:
O fenómeno de compensação referido existe tanto para o som "fundamental" como para as "harmónicas" (e seguindo a mesma lei).
Como é o conjunto "fundamental + harmónicas" que dá o "timbre" do som, este também se mantém.
Que delícia!
Claro que já aqui cheguei perfeitamente fora de horas, na frequência errada e, claro, tudo isso por ter andado, nisto da rede, numa velocidade pouco adequada...
Mas, é isto: Fantástico! (a) Ciência (também) é assim que se faz, não é?
Enviar um comentário
<< Home