Problema irritante - SOLUÇÃO
AQUI está o resumo da solução do problema-infernal, dada por Pólux.
Está de parabéns, pois anda uma multidão de roda dele há uma eternidade!
Ver a explicação detalhada em "Comentário-1"
Está de parabéns, pois anda uma multidão de roda dele há uma eternidade!
Ver a explicação detalhada em "Comentário-1"
Afixado por: Carlos Medina Ribeiro às 08:33
1 Comments:
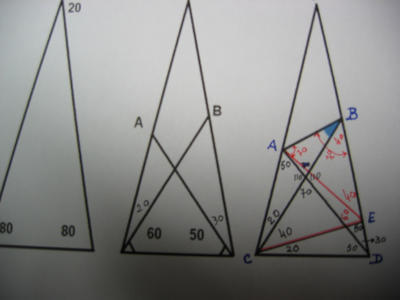
Penso que há uma solução trigonométrica, que entra em conta com semelhança de triângulos, mas creio que a geométrica é preferível, além de mais fácil. Como disse, foi um Prof. meu que, há muito, mostrou à turma a resolução dum problema semelhante (ou seria este, pois não creio que com valores diversos destes seja solúvel).
O triângulo ACD , que tem 2 âng. =s de 50º cada, é isósceles. Donde, AC=CD como se vê na figura colocada por Medina Ribeiro e que deixei, para seguir o raciocínio, na URL :
http://uploads.clix.pt:8080/fotos/data/imagens/2043243/Thumb_43029221EE3F273B9B7D17C3351BA67D17C3.jpg
Desenho agora o triângulo isósceles CDE (2 âng. de 80º nos extremos do lado ED), donde CD=CE
Como AC= CD e CD=CE, então AC=CE . Logo, o triângulo ACE é isóscel es. Como o ângulo ACE mede 60º, os restantes também têm que medir 60º cada um, ou seja, o triângulo ACE é equiláter o (AC=CE=AE). Assim sendo, vou inscrever 60º no ângulo CAE. O ângulo AEB medirá, pois, 40º (180-60), cujo valor inscrevo a vermelho, tal como fiz com o antecedente.
Vamos demonstrar que o triângulo CEB é isósceles. Com efeito, como o ângulo definido em E mede 100 º (60+40), e o definido em C mede 40º (como se retira da figura), então o ângulo B do triângulo CEB também mede 40 º. Inscrevamos o valor a vermelho, para destacar. Logo, CE=BE
Vamos agora demonstrar que o triângulo AEB é, também, isósceles. Como dissemos atrás, AC=CE=AE e CE=BE. Logo, AE=BE o que significa que o triângulo AEB é isósceles. O ângulo definido em E mede 40º, pelo que os ângulos EBA e BAE medem 70º cada. Como o ângulo EBA (70º) é formado pelo “ângulo azul” e pelo ângulo de 40º, a medida correcta do ângulo azul é a diferença entre 70º e 40º, ou seja, 30º.
É muito tarde, pelo que não tenho oportunidade de melhorar o Português ou de corrigir gralhas. Se houver alguma falha, e é natural que a haja, ou algo não for entendido, cá estou para prestar esclarecimentos… se souber.
Com um abraço.
--
Posted by Pólux to sorumbático at 8/17/2005 02:53:13 AM
Enviar um comentário
<< Home