A formiga azarenta e a formiga com sorte
(Não parece, mas é também um problema de Matemática...)
IMAGINE-SE uma corda a que se dá um nó nas duas extremidades e que se coloca no chão de forma confusa, mas sem que haja cruzamentos.A corda está impregnada de insecticida, e uma formiga que esteja no seu interior não consegue sair viva.
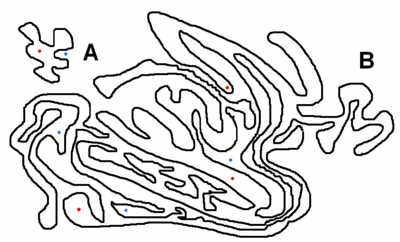No desenho "A", é evidente que a formiga representada a azul está "fora", enquanto a outra está "dentro".Sucede o mesmo (com as da mesma cor) no desenho "B", mas isso já não é tão evidente.
Em princípio, para o verificarmos, é preciso tentar encontrar um caminho de saída - e o problema pode ser indefinidamente complicado com uma extensão de corda maior.
No entanto, há um método fácil que permite, quase de imediato, ver se a formiga se pode salvar ou não. Qual é?
(A Resposta está dada em «Comentário-4»)
Afixado por: Carlos Medina Ribeiro às 12:11
8 Comments:
Mais uma para dar cabo da cabeça à rapaziada!
Mas a avaliar pelo que temos visto, não resiste 2 horas!
Gorjão
Ligar para o Ministério da Ambiente?
Como noutro "post" se refere, o Sr. Ministro do Ambiente tem andado desaparecido.
O certo é que não se lhe dá pela falta, pois não deve haver muitos portugueses que saibam, sequer, o seu nome.
SOLUÇÃO:
Imagina-se (ou traça-se...)uma linha do ponto para o exterior.
Se essa linha interceptar a corda um número ímpar de vezes, é porque a formiga está encerrada no interior.
Inversamente, se o número for par, significa que existe (algures) uma saída.
Uma pequena correcção, ou melhor um complemento à solução:
Se existir pelo menos uma linha que alcance o exterior cruzando a corda um número par de vezes, então existe pelo menos uma saída.
Isto não implica que, se existir uma linha que alcance o exterior um número ímpar de vezes então a formiga esteja encerrada.
Aliás, podem existir inúmeras linhas que alcancem o exterior um número ímpar de vezes, bastando haver uma que cruze a corda um número par de vezes para que a formiga tenha salvação.
Neste caso particular, como só há duas formigas, e pelo enunciado do problema pode-se concluir a não salvação da formiga vermelha, a partir da salvação da formiga azul, que está salva pelo teorema.
Cumprimentos
Neutrolio,
Obrigado pelo seu esclarecimento.
Se puder enviar-me um pequeno exemplo para a sua frase:
«Isto não implica que, se existir uma linha que alcance o exterior um número ímpar de vezes então a formiga esteja encerrada»,
eu podia afixar o desenho.
Este comentário foi removido por um gestor do blogue.
Descobri, agora que o problema dizia, claramente, que a corda tinha as duas pontas unidas. Pelo que a meu post fica sem sentido, já que estava a admitir a hipótese das pontas das cordas poderem estar desunidas.
Sendo assim a afirmação que fiz está incorrecta.
Peço desculpa pelo equívoco.
Cumprimentos
Enviar um comentário
<< Home